Understanding Gradient Descent

Introduction to Gradient Descent

Gradient Descent is a cornerstone optimization algorithm used in machine learning and deep learning to minimize functions and train models effectively. By iteratively adjusting parameters in the direction that reduces a cost function, gradient descent navigates through the landscape of a function to find its minima.

In this article, we’ll explain how gradient descent works, highlight the difference between local and global minima, discuss its shortcomings, and explore advanced variants that address these limitations.

---

How Gradient Descent Works

Gradient Descent minimizes a function $f(x)$ by iteratively updating the parameter $x$ using the formula:

$$x_{t+1} = x_t - \eta \nabla f(x_t)$$

• $x_t$: Current position of the parameter at iteration $t$.
• $\eta$: Learning rate, or step size.
• $\nabla f(x_t)$: Gradient of the function at $x_t$.

The negative gradient ($-\nabla f(x_t)$) points toward the steepest descent, and the learning rate controls how far the algorithm moves at each step.

Example Function

Consider the function:

$$f(x) = 0.1x^3 - 2\sin(x) + 0.5x^2 - 1$$

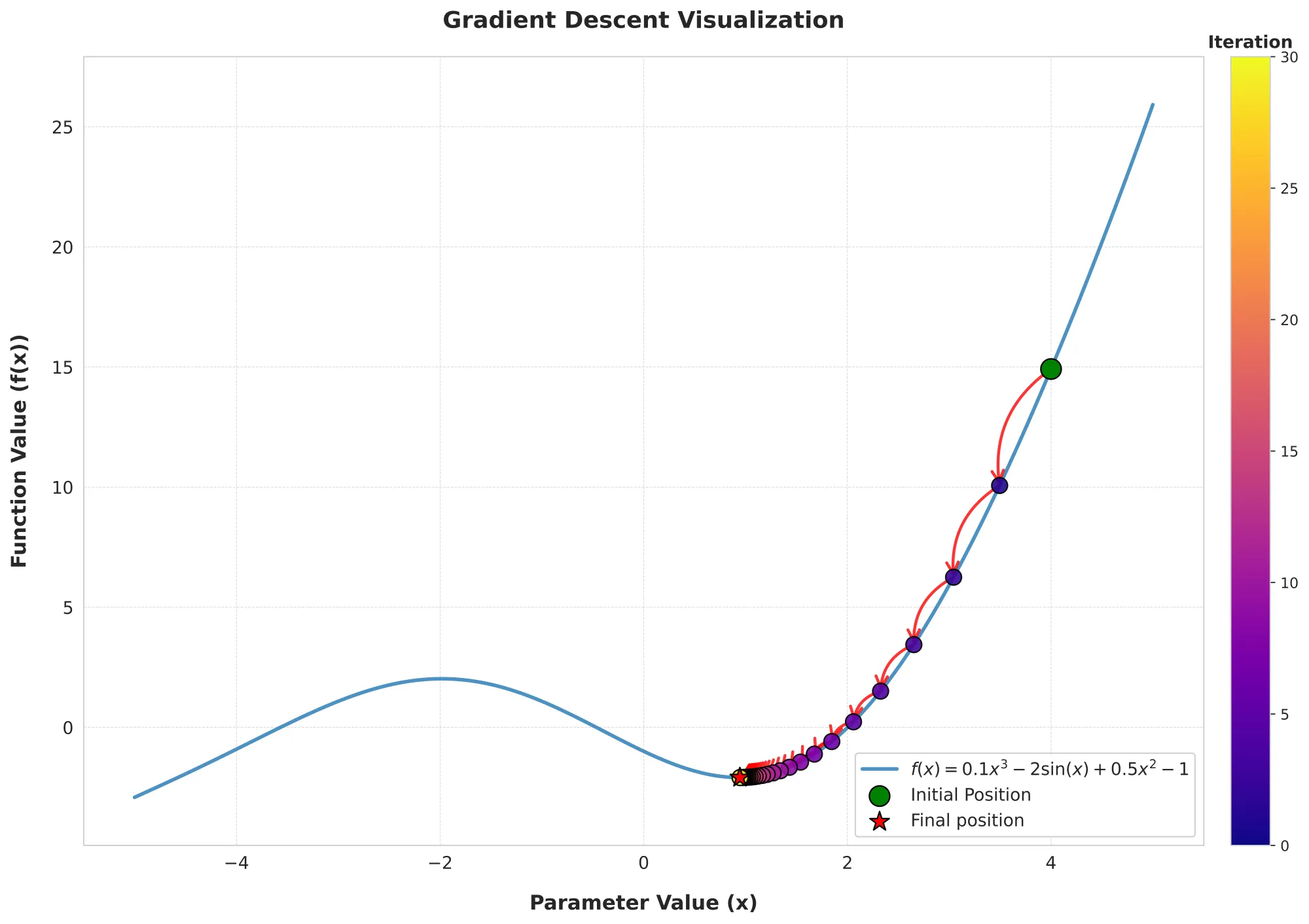
The gradient descent visualization demonstrates how the algorithm iteratively approaches a local minimum. Starting at an initial point (e.g., x = -2), it adjusts $x$ step by step, eventually converging to $x \approx 0.9436$ with $f(x) \approx -2.0901$.

---

Local vs. Global Minima

Local Minimum

A local minimum is a point where the function value is lower than that of nearby points, but it may not be the lowest point overall. In the example function, gradient descent converged to a local minimum because the function is non-convex.

Global Minimum

A global minimum is the absolute lowest point of the function over its entire domain. For non-convex functions, gradient descent may not find the global minimum due to the presence of multiple valleys.

---

Shortcomings of Gradient Descent

1. Local Minima and Saddle Points:

   • Gradient descent may get trapped in a local minimum or saddle point (a flat region where the gradient is near zero but it’s neither a maximum nor a minimum).

2. Learning Rate Sensitivity:

   • A small learning rate slows convergence.
   • A large learning rate risks overshooting or diverging.

3. Non-Convex Functions:

   • For complex, non-convex functions, the algorithm does not guarantee finding the global minimum.

4. Gradient Vanishing/Exploding:

   • Gradients can become too small (vanish) or too large (explode), especially in deep learning scenarios.

---

Advanced Variants of Gradient Descent

Gradient descent has evolved into more advanced techniques to address its limitations, including issues with convergence speed, stability, and susceptibility to local minima. Below are some widely used advanced variants, explained in depth with their respective equations.

---

1. Stochastic Gradient Descent (SGD)

Description

Unlike standard gradient descent, which calculates the gradient using the entire dataset, Stochastic Gradient Descent (SGD) updates the model’s parameters using only a single randomly chosen data point (or a sample) per iteration. This makes it computationally efficient for large datasets.

Update Rule

$$\theta_{t+1} = \theta_t - \eta \nabla_{\theta} J(\theta; x_i, y_i)$$

Where:

• $\theta_t$: Current parameters at iteration $t$
• $\eta$: Learning rate
• $\nabla_{\theta} J(\theta; x_i, y_i)$: Gradient computed for a single data point $(x_i, y_i)$

Advantages

• Faster updates for large datasets.
• Introduces noise into the optimization process, which can help escape local minima.

Limitations

• Noisy convergence can lead to instability.
• May not converge to the exact minimum.

---

2. Mini-Batch Gradient Descent

Description

Mini-Batch Gradient Descent combines the benefits of standard gradient descent and SGD by using a small subset (mini-batch) of data points for each update.

Update Rule

$$\theta_{t+1} = \theta_t - \eta \frac{1}{|B|} \sum_{i \in B} \nabla_{\theta} J(\theta; x_i, y_i)$$

Where:

• $B$: Mini-batch of size $|B|$
• Other terms are as defined in SGD.

Advantages

• Balances speed and convergence stability.
• Reduces memory usage compared to full-batch gradient descent.
• Averages out some noise from SGD.

---

3. Momentum

Description

Momentum adds a fraction of the previous parameter update to the current update, which accelerates convergence in the relevant direction and helps the algorithm bypass local minima or saddle points.

Update Rule

$$v_t = \beta v_{t-1} + (1 - \beta) \nabla_{\theta} J(\theta)$$ $$\theta_{t+1} = \theta_t - \eta v_t$$

Where:

• $v_t$: Velocity (cumulative moving average of gradients)
• $\beta$: Momentum coefficient (typically $0.8 \leq \beta \leq 0.99$)
• Other terms are as defined before.

Advantages

• Accelerates convergence, especially in ravines (areas with steep gradients in one dimension and shallow gradients in another).
• Helps avoid getting stuck in local minima.

---

4. RMSprop (Root Mean Square Propagation)

Description

RMSprop adjusts the learning rate for each parameter dynamically by maintaining a moving average of the squared gradients. This prevents the learning rate from becoming too small or too large.

Update Rule

$$E[g^2]_t = \beta E[g^2]_{t-1} + (1 - \beta) g_t^2$$ $$\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{E[g^2]_t + \epsilon}} g_t$$

Where:

• $E[g^2]_t$: Exponential moving average of squared gradients.
• $g_t$: Gradient at step $t$.
• $\epsilon$: Small constant to prevent division by zero (typically $10^{-8}$).
• $\beta$: Smoothing constant (e.g., $0.9$).

Advantages

• Adapts the learning rate individually for each parameter.
• Suitable for non-stationary objectives and deep learning tasks.

---

5. Adam (Adaptive Moment Estimation)

Description

Adam combines the benefits of Momentum and RMSprop, maintaining both a moving average of the gradients and their squared values. It is one of the most widely used optimizers in deep learning.

Update Rules

1. Compute biased moment estimates: $$m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t$$ $$v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2$$
2. Correct bias in the moment estimates: $$\hat{m}_t = \frac{m_t}{1 - \beta_1^t}, \quad \hat{v}_t = \frac{v_t}{1 - \beta_2^t}$$
3. Update parameters: $$\theta_{t+1} = \theta_t - \frac{\eta \hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon}$$

Where:

• $m_t, v_t$: Biased first and second moment estimates.
• $\beta_1, \beta_2$: Exponential decay rates for the moments (default: $0.9$ and $0.999$).
• $\hat{m}_t, \hat{v}_t$: Bias-corrected estimates.
• $\epsilon$: Small constant (e.g., $10^{-8}$) to prevent division by zero.

Advantages

• Combines the strengths of Momentum and RMSprop.
• Handles sparse gradients well.
• Robust default choice for most deep learning problems.

---

Comparison of Optimizers

Optimizer	Key Feature	Use Case
SGD	Single data point updates	Large datasets
Mini-Batch	Subset of data updates	Balanced speed and stability
Momentum	Adds velocity to updates	Faster convergence, avoids local minima
RMSprop	Adaptive learning rate	Non-stationary objectives
Adam	Combines Momentum & RMSprop	General-purpose deep learning optimizer

Summary

Each variant addresses specific challenges in gradient descent. The choice of optimizer depends on the problem’s nature, dataset size, and computational constraints.

---

Cautionary Notes - Gradient Descent in Practice

1. Local vs. Global Minima:

   • Gradient descent does not guarantee finding the global minimum in non-convex functions. Techniques like initializing from multiple starting points or using global optimization algorithms (e.g., Simulated Annealing, Genetic Algorithms) may help.

2. Learning Rate Tuning:

   • Always experiment with the learning rate. If convergence is too slow, increase it slightly; if it oscillates, reduce it. Techniques like learning rate schedules (decreasing the learning rate over time) can improve performance.

3. Feature Scaling:

   • Ensure input features are normalized or standardized. Unscaled features can distort gradient calculations, leading to slow or incorrect convergence.

4. Visualization Helps:

   • As seen in the plot, visualizing the function and optimization path helps understand convergence behavior and identify issues like getting stuck in a local minimum.

---

Conclusion

Gradient Descent is an essential tool in optimization, powering countless machine learning and deep learning algorithms. While it has its limitations—like susceptibility to local minima and sensitivity to learning rates—advanced variants such as Adam and RMSprop help address these challenges.

Understanding the trade-offs between local and global minima, and carefully tuning hyperparameters, are key to making the most of gradient descent. Visualizing the process, as shown in the reference plot, provides valuable insights into the algorithm’s behavior.