Activation And Loss Functions In Deep Learning • Neural Nets

Activation and loss functions are fundamental components in deep learning architectures. They play crucial roles in both the forward propagation of signals and the backward propagation of gradients during model training. This article provides an in-depth analysis of common activation and loss functions, their mathematical foundations, and practical applications.

Activation Functions

Activation functions introduce non-linearity into neural networks, enabling them to learn complex patterns. Let’s examine key activation functions and their properties.

1. Rectified Linear Unit (ReLU)

The ReLU function is currently the most widely used activation function in deep learning. Its popularity stems from its computational efficiency and effectiveness in addressing the vanishing gradient problem.

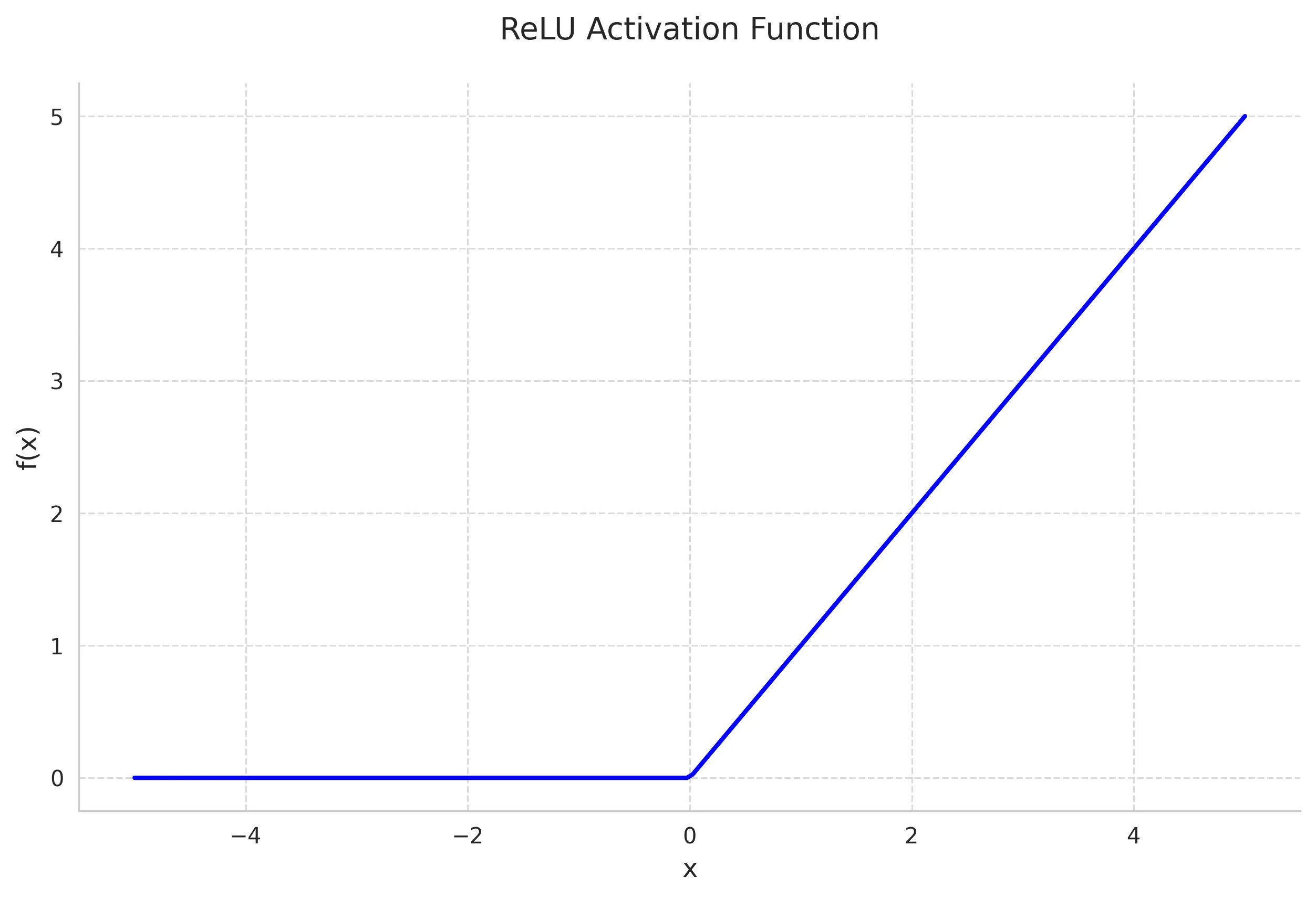
Mathematical Definition:

f(x) = \max(0, x) = \begin{cases} x & \text{if } x > 0 \\ 0 & \text{if } x \leq 0 \end{cases}

Derivative:

f'(x) = \begin{cases} 1 & \text{if } x > 0 \\ 0 & \text{if } x < 0 \\ \text{undefined} & \text{if } x = 0 \end{cases}

Key Properties:

Non-saturating for positive values
Sparse activation (approximately 50% of neurons are typically active)
Computationally efficient
Helps mitigate vanishing gradient problem

Use Cases:

Default choice for hidden layers in deep neural networks
Particularly effective in Convolutional Neural Networks (CNNs)
Computer vision applications
Deep architectures with many layers

2. Leaky ReLU

Leaky ReLU addresses the “dying ReLU” problem by allowing a small gradient when the unit is not active.

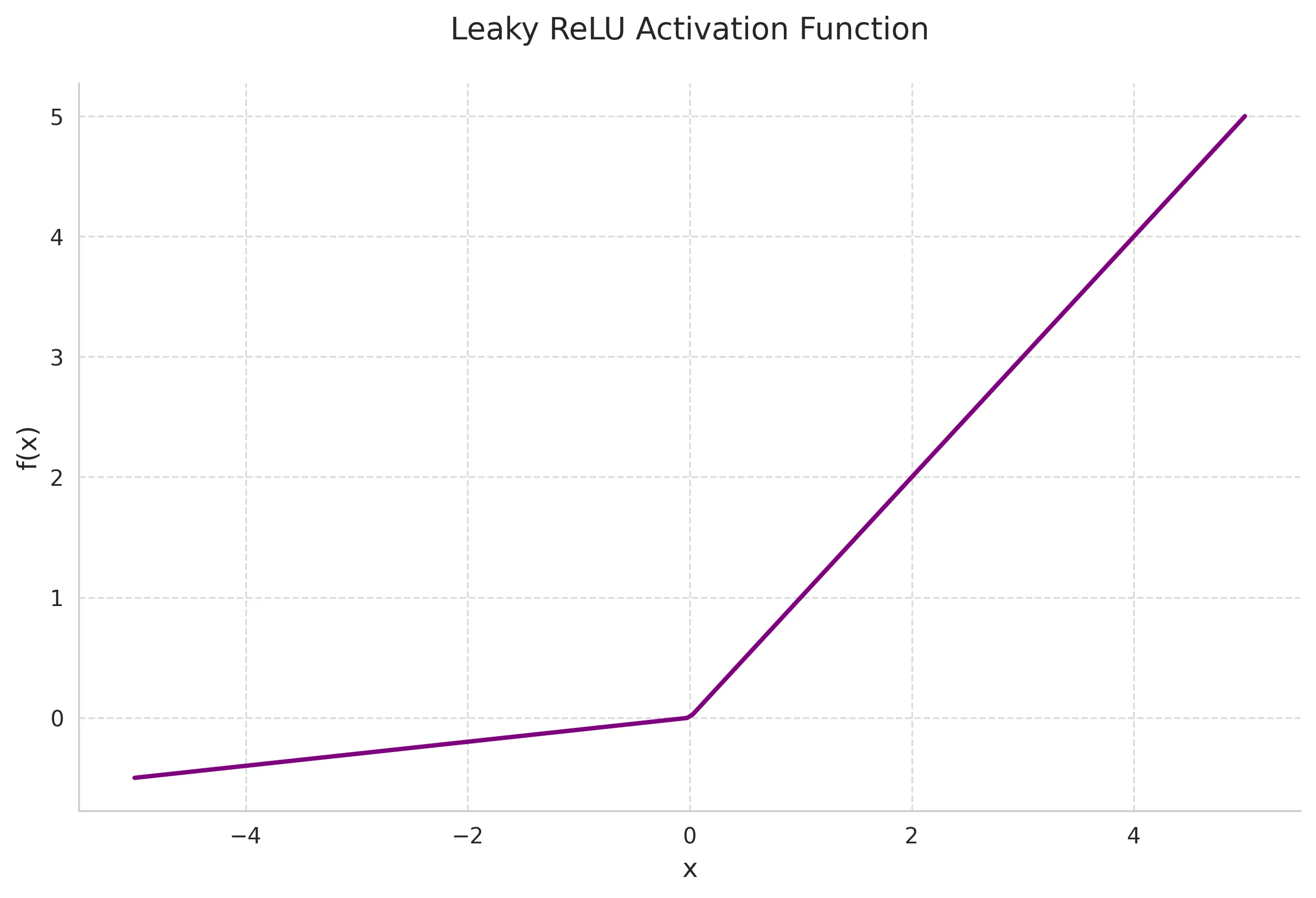
Mathematical Definition:

f(x) = \begin{cases} x & \text{if } x > 0 \\ \alpha x & \text{if } x \leq 0 \end{cases}

where $\alpha$ is typically a small constant like 0.01.

Derivative:

f'(x) = \begin{cases} 1 & \text{if } x > 0 \\ \alpha & \text{if } x < 0 \end{cases}

Key Properties:

Prevents dead neurons
Allows negative gradients
Generally maintains the benefits of ReLU
Parameter $\alpha$ can be learned (Parametric ReLU)

Use Cases:

Alternative to ReLU when dead neurons are a concern
Deep networks where gradient flow is critical
Tasks requiring negative value preservation

3. Sigmoid Function

The sigmoid function maps inputs to values between 0 and 1, making it useful for probability-based predictions.

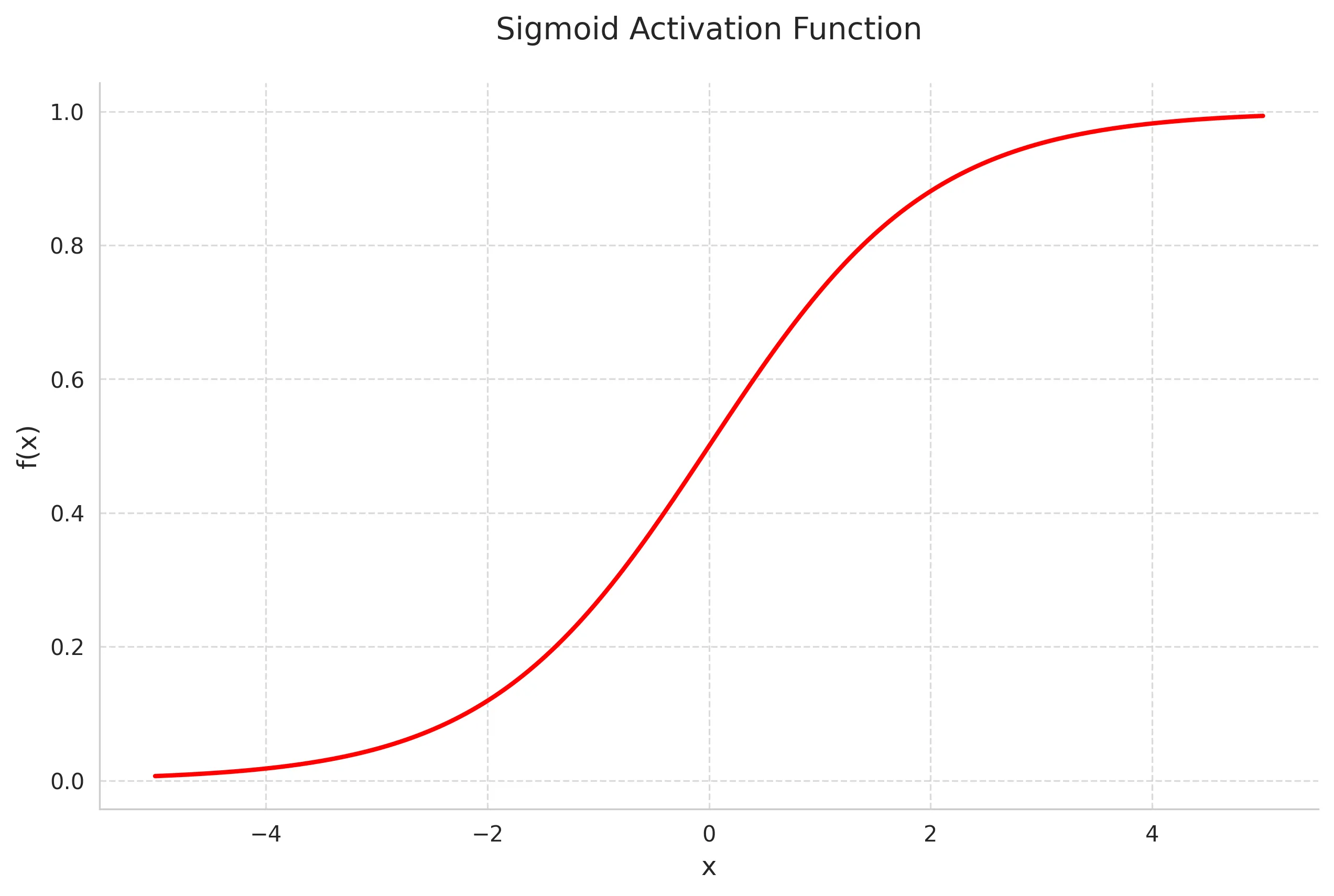
Mathematical Definition:

f(x) = \frac{1}{1 + e^{-x}}

Derivative:

f'(x) = f(x)(1 - f(x))

Key Properties:

Output range (0,1)
Smooth gradient
Clear probabilistic interpretation
Suffers from vanishing gradient for extreme values

Use Cases:

Binary classification output layers
Gates in LSTM and GRU units
Probability estimation tasks
Legacy networks (historically popular)

4. Hyperbolic Tangent (tanh)

Tanh is a scaled and shifted version of the sigmoid function, mapping inputs to the range (-1,1).

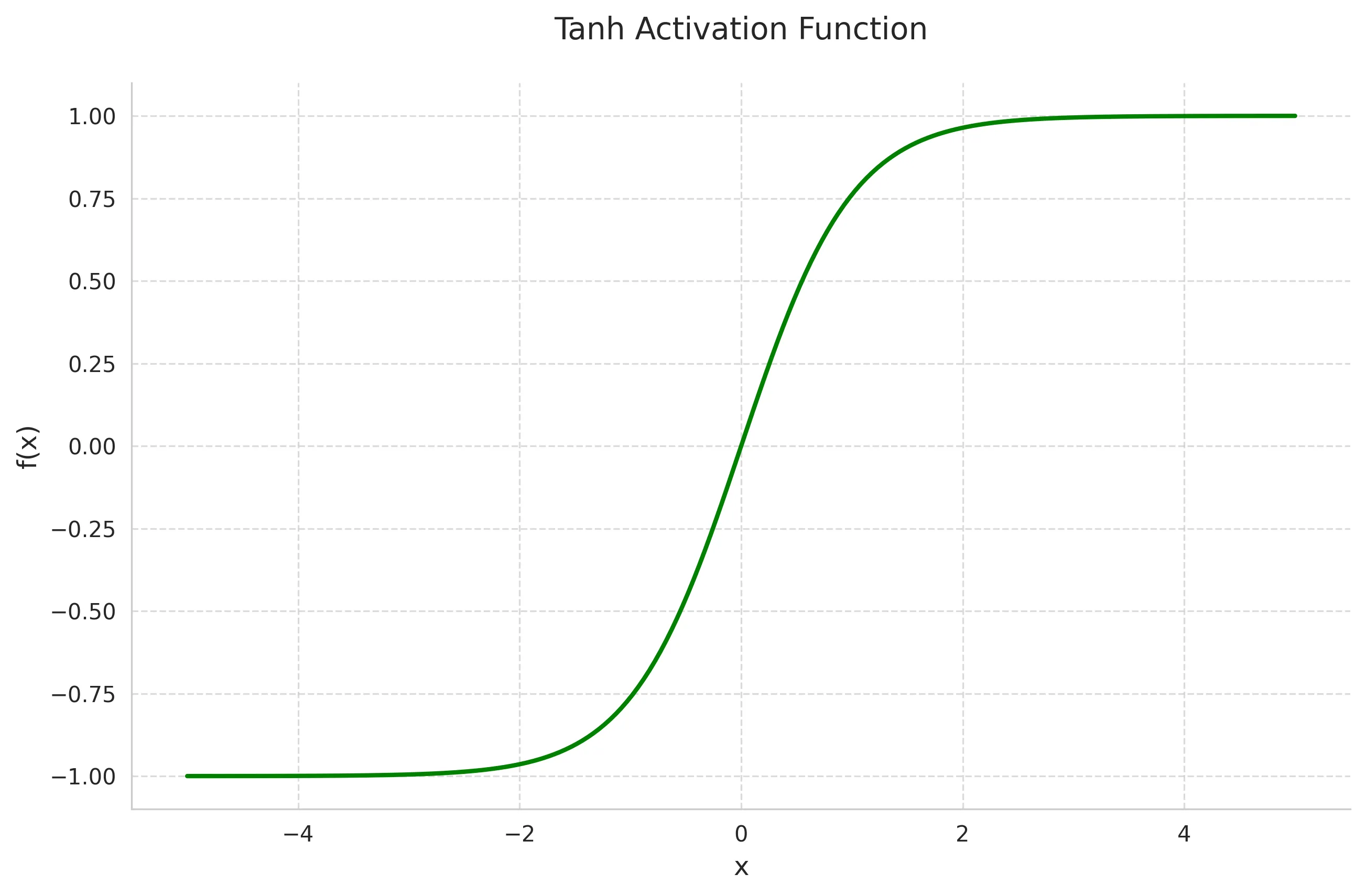
Mathematical Definition:

f(x) = \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}

Derivative:

f'(x) = 1 - \tanh^2(x)

Key Properties:

Output range (-1,1)
Zero-centered
Stronger gradients compared to sigmoid
Still suffers from vanishing gradient at extremes

Use Cases:

Hidden layers in shallow networks
NLP tasks
LSTM/GRU internal states
Cases requiring normalized outputs

5. Softmax Function

The softmax function generalizes the logistic function to handle multiple classes, converting a vector of values into a probability distribution.

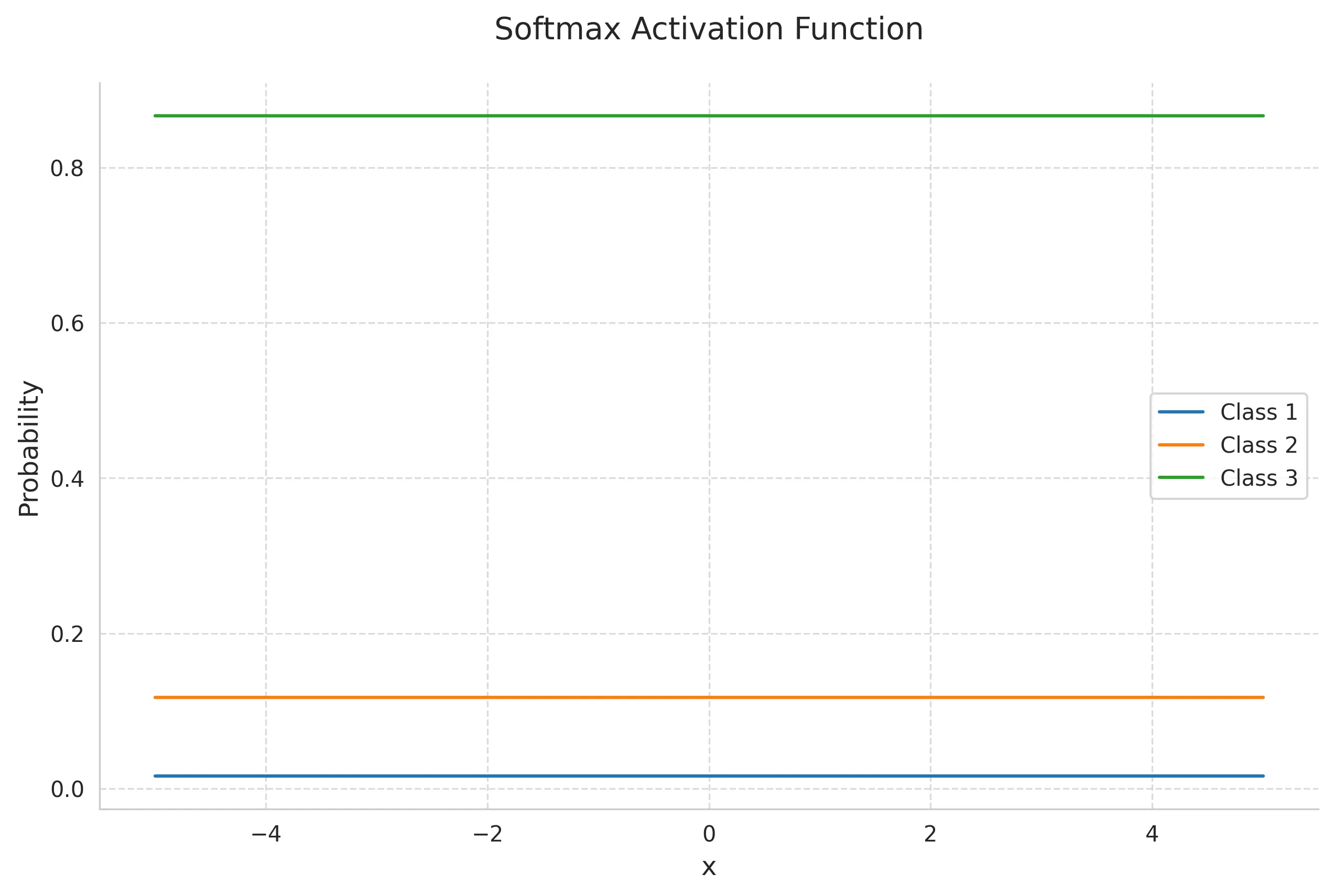
Mathematical Definition: For a K-dimensional vector x:

\text{softmax}(x_i) = \frac{e^{x_i}}{\sum_{j=1}^K e^{x_j}}

Derivative: For i = j

\frac{\partial \text{softmax}(x_i)}{\partial x_j} = \text{softmax}(x_i)(1 - \text{softmax}(x_i))

and For i ≠ j

\frac{\partial \text{softmax}(x_i)}{\partial x_j} = -\text{softmax}(x_i)\text{softmax}(x_j)

Key Properties:

Outputs sum to 1
Squashes values to range (0,1)
Preserves relative ordering
Differentiable
Emphasizes largest values while suppressing lower ones

Use Cases:

Multi-class classification output layers
Attention mechanisms in transformers
Policy networks in reinforcement learning
Probability distribution generation

6. Exponential Linear Unit (ELU)

ELU provides smoother gradients compared to ReLU variants while maintaining most of their benefits.

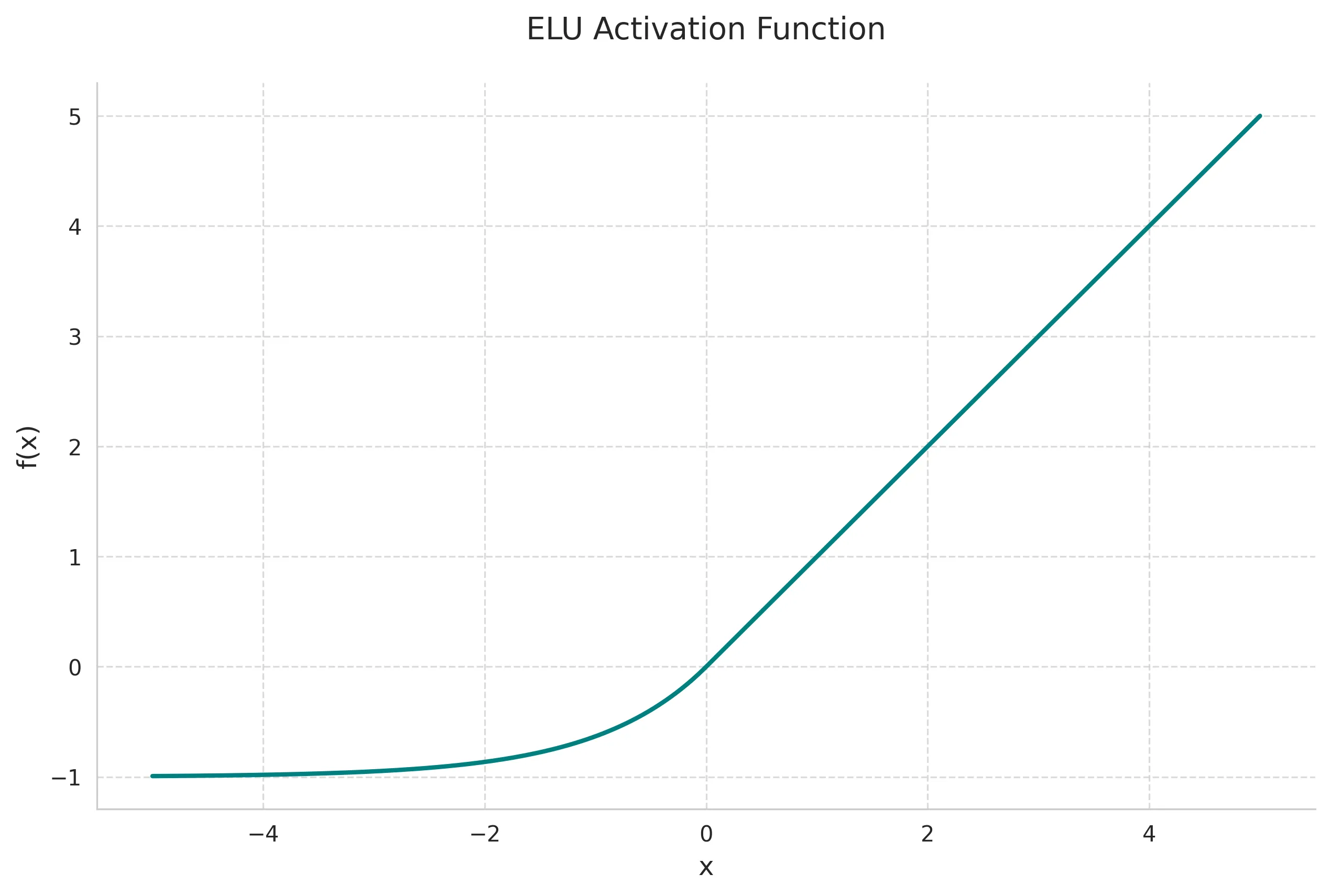
Mathematical Definition:

f(x) = \begin{cases} x & \text{if } x > 0 \\ \alpha(e^x - 1) & \text{if } x \leq 0 \end{cases}

Derivative:

f'(x) = \begin{cases} 1 & \text{if } x > 0 \\ \alpha e^x & \text{if } x \leq 0 \end{cases}

Key Properties:

Smooth function including negative values
Reduces bias shift
Self-regularizing properties
Computationally more expensive than ReLU

Use Cases:

Deep neural networks requiring smooth gradients
Tasks sensitive to negative values
Networks requiring strong regularization
Alternative to batch normalization

7. Scaled Exponential Linear Unit (SELU)

SELU enables self-normalizing properties in neural networks, automatically pushing activations toward zero mean and unit variance.

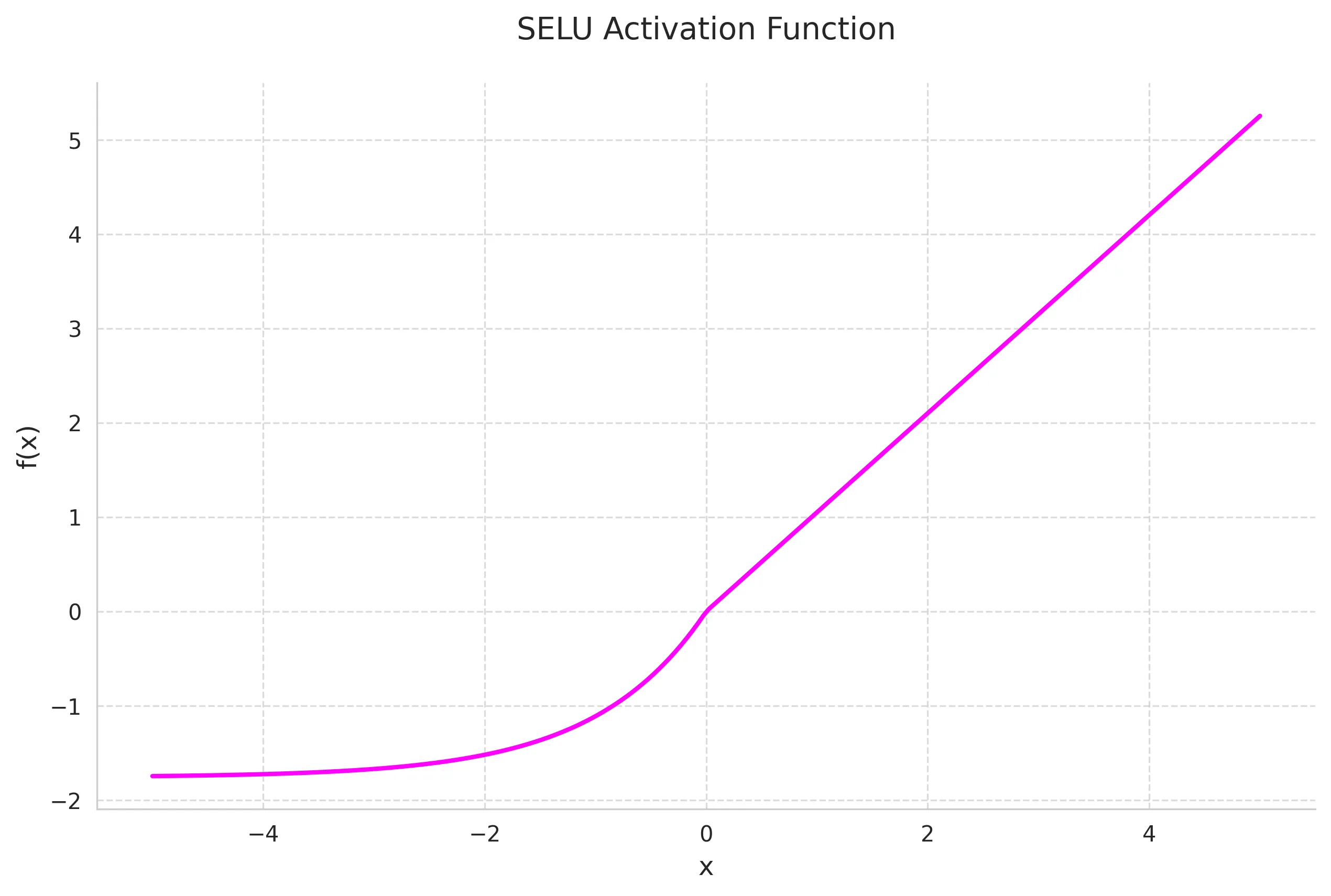
Mathematical Definition:

f(x) = \lambda \begin{cases} x & \text{if } x > 0 \\ \alpha(e^x - 1) & \text{if } x \leq 0 \end{cases}

where: $\alpha \approx 1.676$ $\lambda \approx 1.0507$

Key Properties:

Self-normalizing
Maintains consistent mean and variance
Robust to perturbations
Requires specific initialization (LeCun normal)

Use Cases:

Deep networks without batch normalization
Networks requiring stable training
Applications with limited computational resources
Tasks requiring strong regularization

Loss Functions

Loss functions quantify the difference between predicted and actual values, guiding the optimization process during training.

1. Mean Squared Error (MSE)

MSE is the most common loss function for regression tasks.

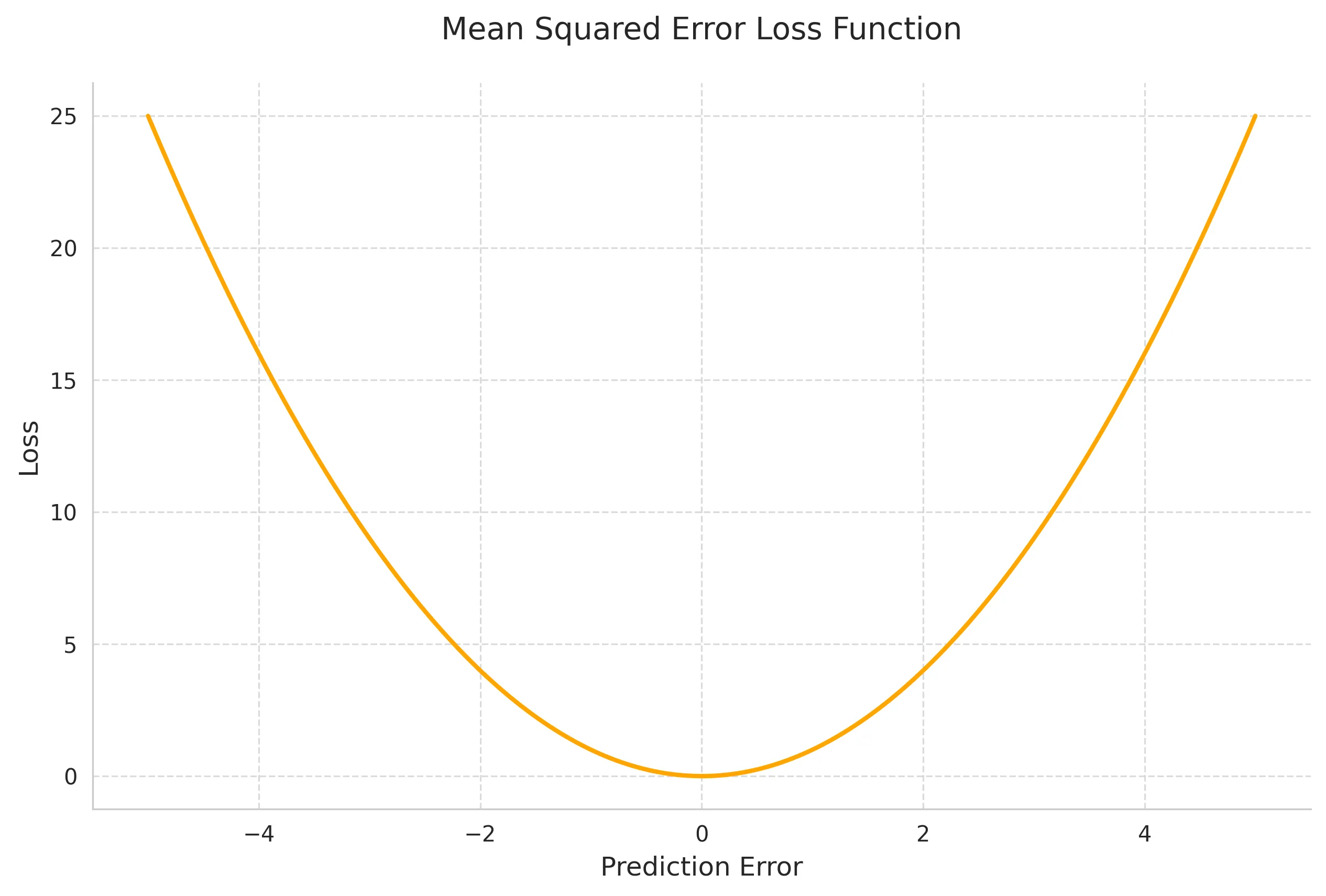
Mathematical Definition:

\text{MSE} = \frac{1}{n}\sum_{i=1}^n (y_i - \hat{y}_i)^2

Derivative:

\frac{\partial \text{MSE}}{\partial \hat{y}_i} = -\frac{2}{n}(y_i - \hat{y}_i)

Key Properties:

Heavily penalizes large errors
Differentiable everywhere
Non-negative
Convex function
Sensitive to outliers

Use Cases:

Regression problems
When outliers are rare or meaningful
When large errors should be heavily penalized
Signal processing applications

2. Binary Cross-Entropy Loss

Binary Cross-Entropy (BCE) is fundamental for binary classification tasks, measuring the difference between predicted probabilities and true binary labels.

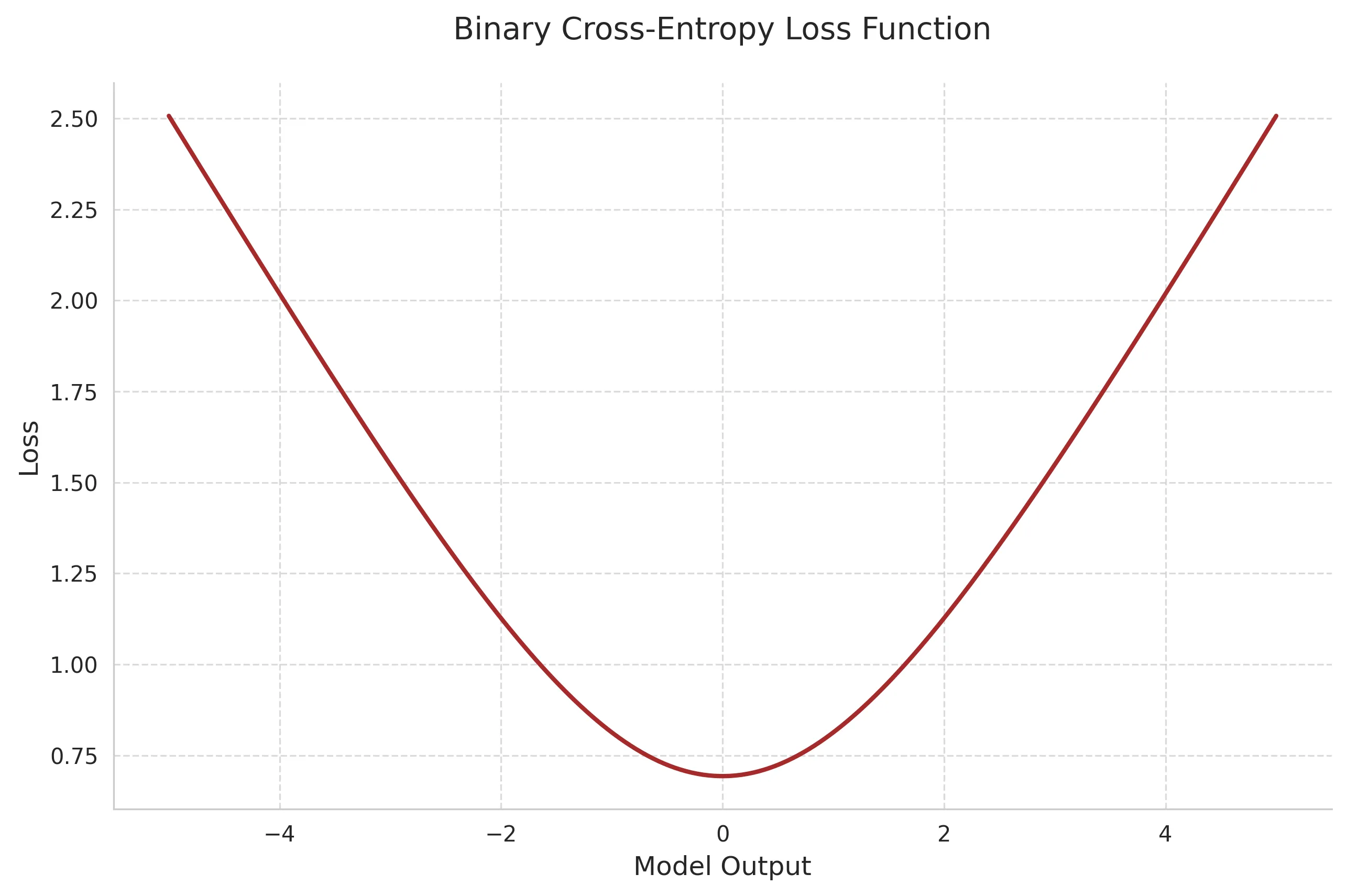
Mathematical Definition:

\text{BCE} = -\frac{1}{N}\sum_{i=1}^N [y_i \log(\hat{y}_i) + (1-y_i)\log(1-\hat{y}_i)]

where:

$y_i$ is the true label (0 or 1)
$\hat{y}_i$ is the predicted probability
$N$ is the number of samples

Derivative with respect to logits (before sigmoid):

\frac{\partial \text{BCE}}{\partial x} = \sigma(x) - y

where $\sigma(x)$ is the sigmoid function.

Key Properties:

Bounded between 0 and ∞
Provides stronger gradients than MSE for probabilities
Works well with probabilistic predictions
Natural pairing with sigmoid activation

Use Cases:

Binary classification
Generative Adversarial Networks (GANs)
Anomaly detection
Multi-label classification (per-label)

3. Focal Loss

Focal Loss addresses class imbalance by down-weighting easy examples and focusing on hard ones.

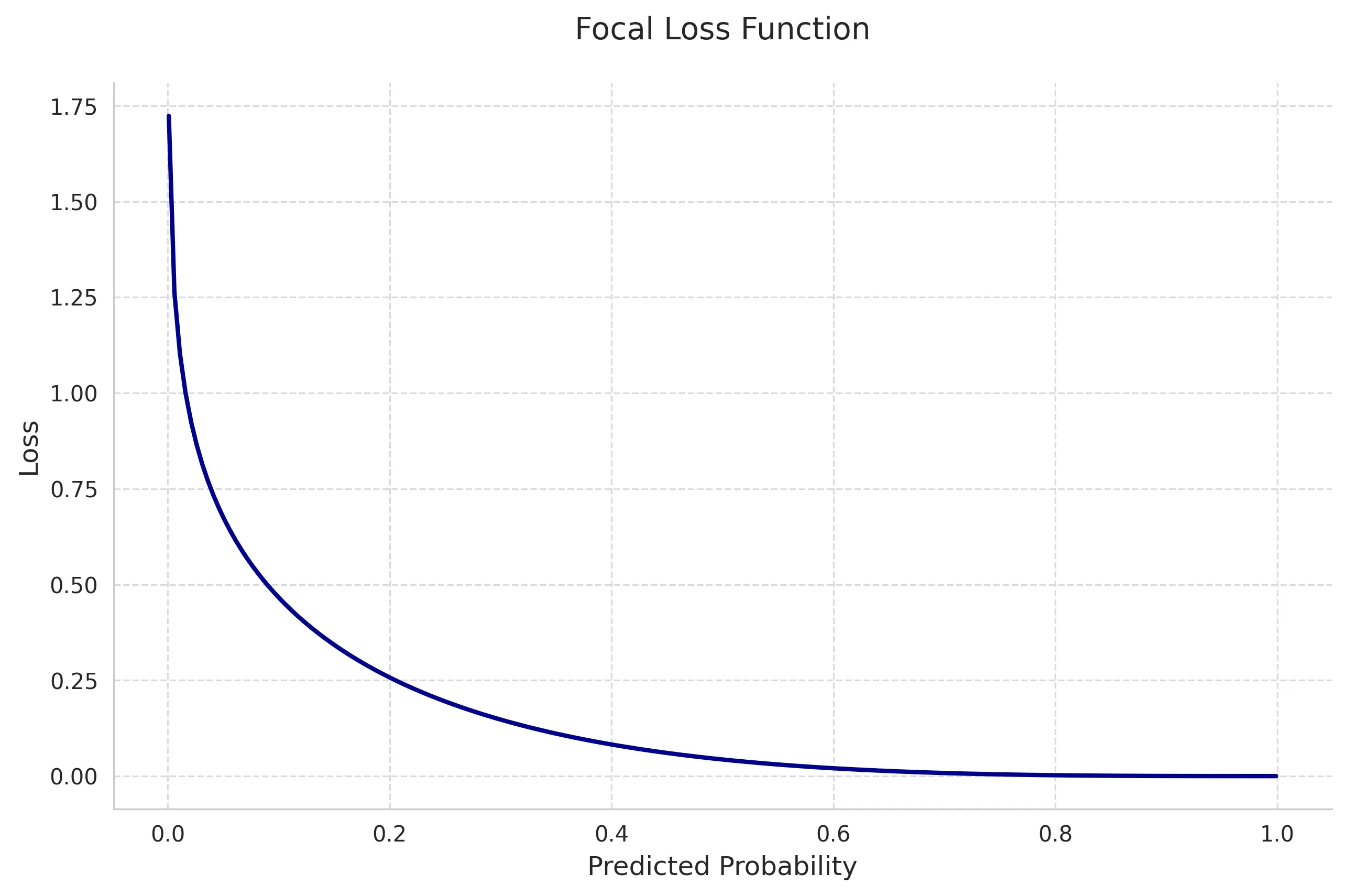
Mathematical Definition:

\text{FL}(p_t) = -\alpha_t(1-p_t)^\gamma \log(p_t)

where:

$p_t$ is the model’s estimated probability for the true class
$\gamma$ is the focusing parameter (typically 2)
$\alpha_t$ is the class balancing factor

Key Properties:

Reduces impact of easy examples
Automatically handles class imbalance
Tunable focus on hard examples via $\gamma$
Generalizes cross-entropy loss ( $\gamma = 0$ )

Use Cases:

Object detection
Highly imbalanced datasets
Dense prediction tasks
Medical image segmentation

4. Huber Loss

Huber Loss combines the best properties of MSE and Mean Absolute Error (MAE), being less sensitive to outliers than MSE while maintaining differentiability.

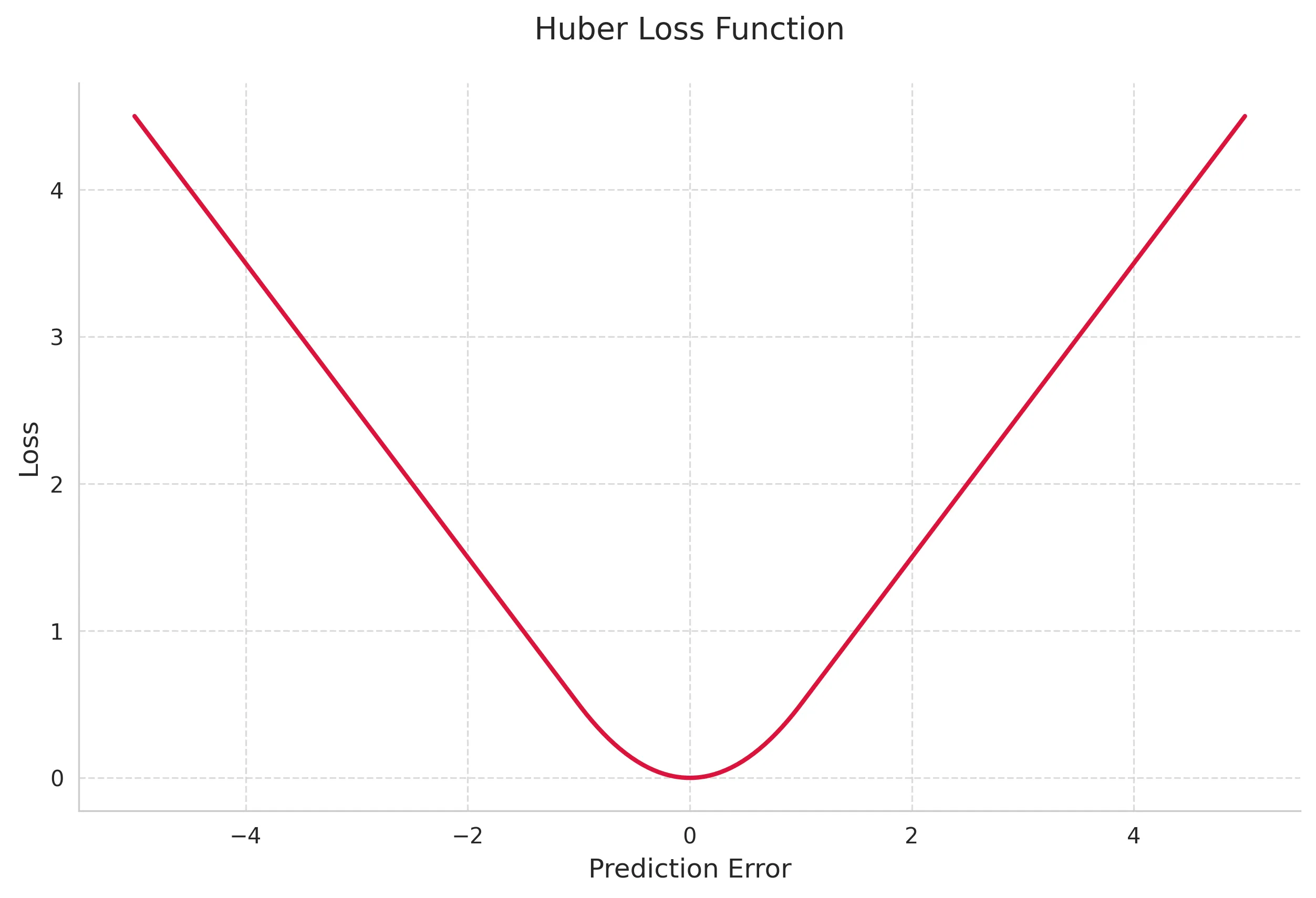
Mathematical Definition:

L_\delta(y, \hat{y}) = \begin{cases} \frac{1}{2}(y - \hat{y})^2 & \text{for } |y - \hat{y}| \leq \delta \\ \delta|y - \hat{y}| - \frac{1}{2}\delta^2 & \text{otherwise} \end{cases}

Derivative:

\frac{\partial L_\delta}{\partial \hat{y}} = \begin{cases} y - \hat{y} & \text{for } |y - \hat{y}| \leq \delta \\ \delta \cdot \text{sign}(y - \hat{y}) & \text{otherwise} \end{cases}

Key Properties:

Combines MSE and MAE benefits
Robust to outliers
Differentiable everywhere
Adjustable sensitivity via $\delta$

Use Cases:

Regression with outliers
Robust optimization
Reinforcement learning
Time series prediction

5. Hinge Loss

Hinge Loss is primarily used in Support Vector Machines and margin-based learning.

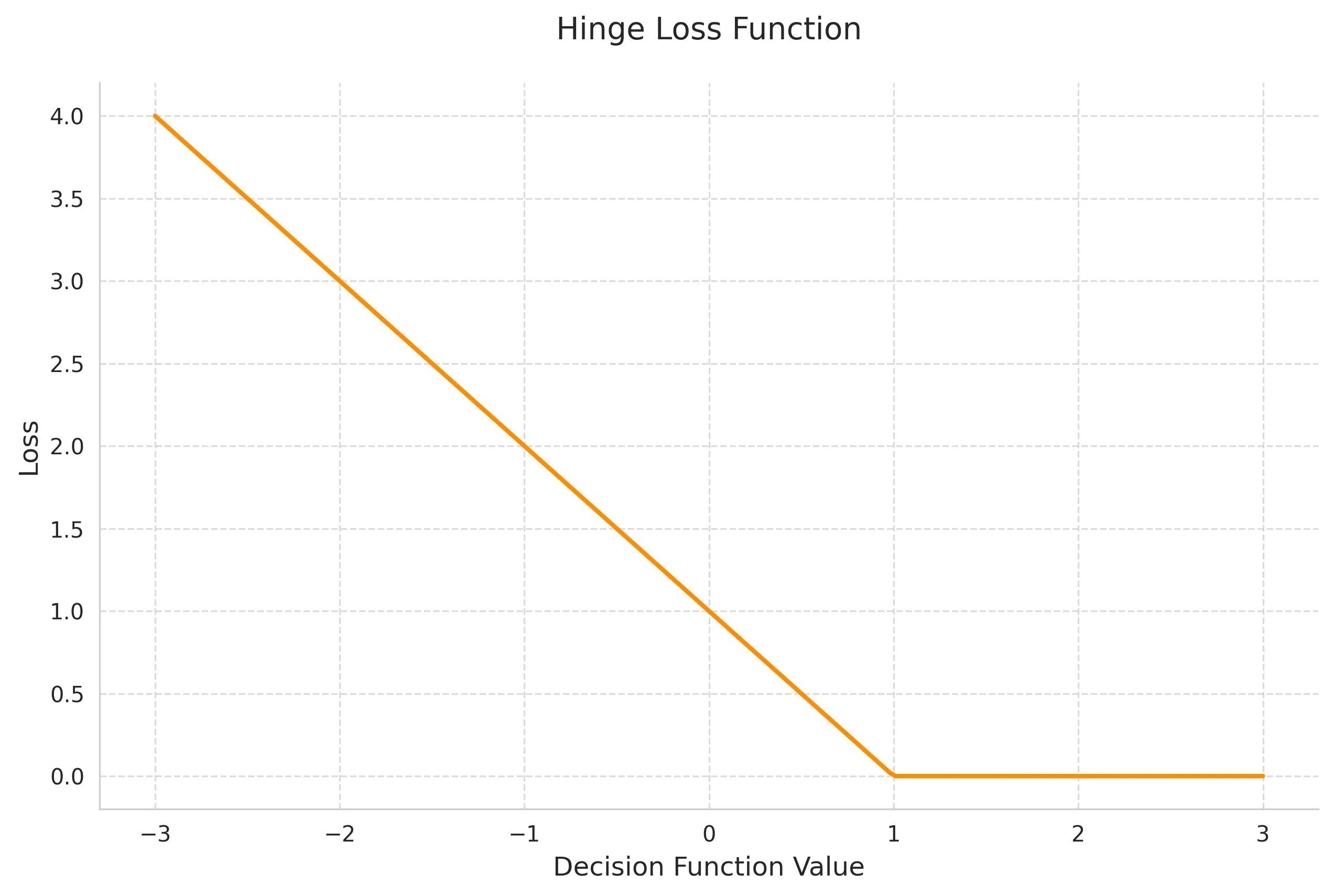
Mathematical Definition:

L(y, \hat{y}) = \max(0, 1 - y\hat{y})

where $y \in \{-1, 1\}$ and $\hat{y}$ is the model’s prediction.

Key Properties:

Maximum margin classification
Non-differentiable at hinge point
Sparse gradients
Focus on margin violations

Use Cases:

Support Vector Machines
Maximum margin classifiers
Structured prediction
Online learning algorithms

Code Samples

For Activation Functions

import numpy as np
import tensorflow as tf

# Activation Functions

# 1. ReLU
def relu(x):
    return tf.nn.relu(x)  # or np.maximum(0, x) for NumPy

# 2. Leaky ReLU
def leaky_relu(x, alpha=0.01):  # alpha is the leak coefficient
    return tf.maximum(alpha * x, x) # or np.where(x > 0, x, x * alpha) for NumPy


# 3. Sigmoid
def sigmoid(x):
    return tf.sigmoid(x) # or 1 / (1 + np.exp(-x)) for NumPy


# 4. Tanh
def tanh(x):
    return tf.tanh(x) # or np.tanh(x) for NumPy


# 5. Softmax
def softmax(x):
    return tf.nn.softmax(x) # or np.exp(x) / np.sum(np.exp(x), axis=-1, keepdims=True) for NumPy


# 6. ELU (Exponential Linear Unit)
def elu(x, alpha=1.0):  # alpha is a hyperparameter
  return tf.nn.elu(x)  # TensorFlow handles ELU directly


# 7. SELU (Scaled Exponential Linear Unit)
def selu(x):
    alpha = 1.673
    scale = 1.0507
    return scale * tf.where(x >= 0.0, x, alpha * tf.exp(x) - alpha)

For Loss Functions

# 1. MSE (Mean Squared Error)
def mse(y_true, y_pred):
    return tf.reduce_mean(tf.square(y_true - y_pred)) # or np.mean(np.square(y_true - y_pred)) for NumPy

# 2. Binary Cross-Entropy
def binary_crossentropy(y_true, y_pred):
    return tf.reduce_mean(tf.keras.losses.binary_crossentropy(y_true, y_pred))

# 3. Focal Loss (requires a bit more setup)
def focal_loss(y_true, y_pred, gamma=2.0, alpha=0.25):
    y_pred = tf.clip_by_value(y_pred, 1e-7, 1.0 - 1e-7) # avoid numerical instability
    pt_1 = tf.where(tf.equal(y_true, 1), y_pred, tf.ones_like(y_pred))
    pt_0 = tf.where(tf.equal(y_true, 0), y_pred, tf.zeros_like(y_pred))
    return -tf.reduce_sum(alpha * tf.pow(1. - pt_1, gamma) * tf.math.log(pt_1)) - tf.reduce_sum((1 - alpha) * tf.pow(pt_0, gamma) * tf.math.log(1. - pt_0))

# 4. Huber Loss
def huber_loss(y_true, y_pred, delta=1.0):
    return tf.reduce_mean(tf.keras.losses.huber(y_true, y_pred, delta=delta))

# 5. Hinge Loss
def hinge_loss(y_true, y_pred):  # For multi-class, use categorical_hinge
    return tf.reduce_mean(tf.keras.losses.hinge(y_true, y_pred))

Example of using the functions (TensorFlow)

x = tf.constant([-2.0, -1.0, 0.0, 1.0, 2.0])
print("ReLU:", relu(x))

y_true = tf.constant([0, 1, 0, 1, 1])
y_pred = tf.constant([0.1, 0.9, 0.2, 0.8, 0.7])
print("Binary Cross-Entropy:", binary_crossentropy(y_true, y_pred).numpy())


# Example with NumPy (replace tf functions with their NumPy equivalents
x_np = np.array([-2.0, -1.0, 0.0, 1.0, 2.0])
print("NumPy ReLU:", np.maximum(0, x_np))


y_true_np = np.array([0, 1, 0, 1, 1])
y_pred_np = np.array([0.1, 0.9, 0.2, 0.8, 0.7])
print("NumPy MSE:", np.mean(np.square(y_true_np - y_pred_np)))

Activation-Loss Pairings

Common effective combinations:

Softmax + Categorical Cross-Entropy
Sigmoid + Binary Cross-Entropy
Linear + MSE/Huber
ReLU/ELU + Any Loss (hidden layers)

Conclusion

The activation and loss functions are foundational to deep learning models. Activation functions introduce non-linearity and control the signal flow, while loss functions guide the optimization process, quantifying the difference between predictions and target values. The choice of these functions directly impacts a model’s convergence rate, accuracy, and overall performance on specific tasks.